Tidskonstant

Tidskonstanten (tau) fortæller hvor hurtig processen er. En stor tidskonstant betyder en langsom proces og en lille tidskonstant betyder at processen er hurtig. Tidskonstanten defineres som den tid der går fra et Trin-Input gives til processen indtil Trin-Svaret har nået 63,2% af sit slutværdi eller det stationære værdi (udgangssignalet bliver ikke større). Hvordan findes så tidskonstant for en given proces? Figuren her forneden viser en vilkårlig, ukendt proces og skal tidskonstanten findes for denne proces.

Figur 1 – Vilkårlig process

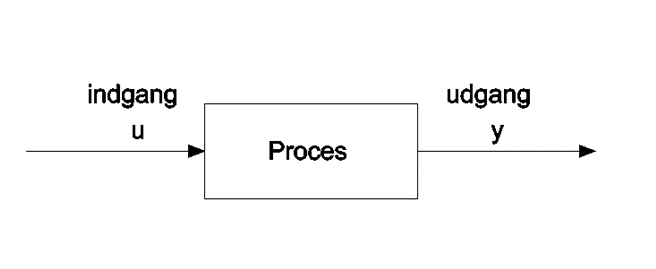
Her er u indgangssignalet og y er udgangssignalet. Til at finde tidskonstanten giver vi et Trin-Input til processen (u) og undersøger Trin-Svaret (y). Dette vises på figuren her forneden.

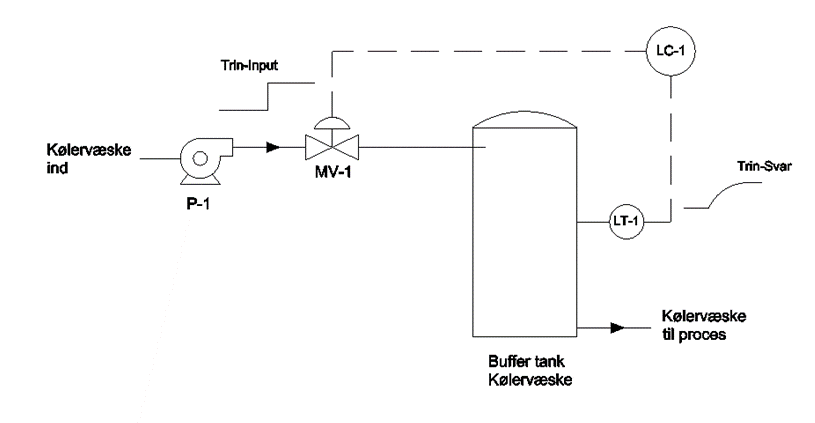
Figur 2 – Trin-Input og Trin-Svar for en Buffertank

Trin-Input til denne proces fås med at ændre indstillingerne til ventilen (MV-1) med regulatoren i manual mode, og undersøge Trin-Svaret der aflæses fra LT-1. Nu undersøges Trin-Svaret til at finde tidskonstanten. Trin-Input og Trin-Svar undersøges i det samme graf, se her forneden.

Figur 3 – Trins-Input og Trin-Svar

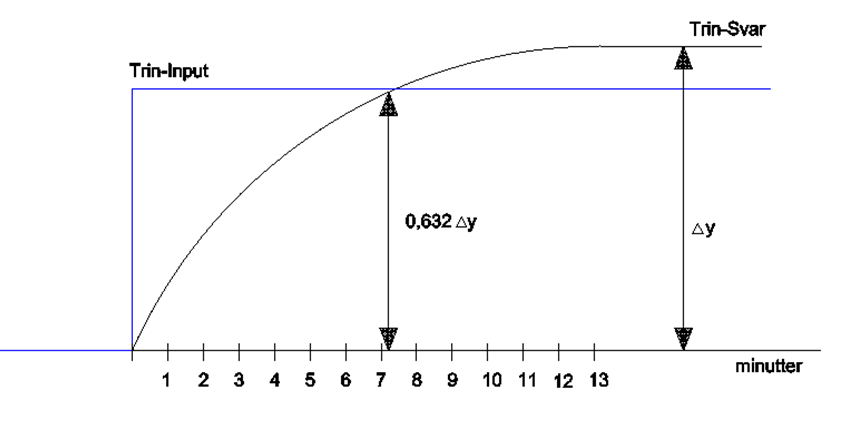
Fra figur 3 kan vi se at tidskonstanten aflæses til at være ca. 7,2 minutter.

Huskeregler:

  • Tidskonstant findes for en første ordens proces. I en anden ordens proces findes der 2 tidskonstanter og så er der kun den “rådende” tidskonstant der kan findes med et Trin-Input.
  • Undersøg altid tidskonstanten i arbejdsområdet for det er der den spiller en rolle. I buffertanken kan området være fra 40% – 60% og ønskeværdien 50%. Her giver det ingen mening at bruge Trin-Input fra 0 – 100%.
  • Giv aldrig for stort Trin-Input. Lær processen at kende eller tal med en der kender processen før der gives et Trin-Input.
  • Det er ikke altid nemt, og måske ikke nødvendigt, at bestemme tidskonstanten med stor nøjagtighed, da det målte signal ofte er svært at arbejde med. Brug det bedste estimat for tidskonstanten.

Tidskonstant – beregninger

Nu introduceres matematikken bag tidskonstanten for en første ordens proces. IKKE FÆRDIGLAVET.

 
En første orden proces kan bedst beskrives med en første ordens differentialligning


 (1)    \begin{equation*}  \tau \frac{dy(t)}{dt} +y(t) = K_p\cdot u(t)  \qquad  med \qquad y(0) = 0 \end{equation*}
 
Her står \tau for tidskonstanten, y(t) for (Trin-Respons), u(t) for Trin-Input og K_p for Proces forstærkningen. 

  
Ligningen kan også skrives på følgende måde


 (2)    \begin{equation*}   \tau \frac{dy(t)}{dt} +y(t) = K_p\cdot K_A  \qquad  med \qquad y(0) = 0  \end{equation*}
 
Her navngives u(t) til K_A som er det konstant værdi der gives på indgangen af systemet, efter Trin-Input.

Nu løses denne differentiale ligning til at finde tidskonstanten.

   
Der divideres på begge sider af lighedstegnet tidskonstanten \tau og isolerer \frac{dy(t)}{dt}


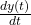
 (3)    \begin{equation*}    \frac{dy(t)}{dt} +\frac{1}{\tau} y(t) = \frac{K_p\cdot K_A}{\tau}      \end{equation*}
  


 (4)    \begin{equation*}    \frac{dy(t)}{dt} =  \frac{K_p\cdot K_A}{\tau} -\frac{1}{\tau} y(t)      \end{equation*}
  

Den fuldstændige løsning kan nu aflæses fra tabeller (ligningen kan selvfølgelige løses direkte).

Her forneden vises der tabel med differentiale ligninger samt fuldstændige løsninger til disse.

Løsning til differentiale ligninger. Kilde webmatematik.dk
   
Her kan den fuldstændige løsning for differentiel ligningen aflæses. 


 (5)    \begin{equation*}     $y'$ = b - a\cdot y \qquad har\  løsningen \qquad  y(t) = \frac{b}{a} +c \cdot e^{(-a\cdot x)}       \end{equation*}
   

Omskrives for ligning 4, med b = \frac{K_p\cdot K_A}{\tau} og a = \frac{1}{\tau}


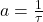
 (6)    \begin{equation*}    y(t) =  K_p\cdot K_A + c \cdot e^{\frac{-t}{\tau}}         \end{equation*}
  

Nu skal konstanten c findes med at indsætte begyndelsesbetingelserne i ligningen.  Til tiden t = 0 er y(0) = 0 (ikke noget trin-respons) så ligning kan omskrives til


 (7)    \begin{equation*}    y(0) =  K_p\cdot K_A + c \cdot e^{\frac{0}{\tau}} \end{equation*}
  

Som giver


 (8)    \begin{equation*}    c =  -K_p\cdot K_A  \end{equation*}
Scroll to Top